Détails: Catégorie : Programmation Python - STAV; Mis à jour : 12 décembre 2020; Affichages : 12727

Index de l'article

Objectif

Support de cours présenté sur le premier trimestre 2020-2021 à destination des Terminales Générales du lycée sur demande des enseignants de Phys et Maths. Normalement dans le cadre d'HSE - demande en cours - 20h - obtenu 15h

Ne sachant pas où le déposer, je me dis qu'ici il pourra être consulté par des bac techno aussi.

Table des matières

1 - Sources inspirantes
2 - Introduction
3 - Présentation de l’IDE Thonny
4 - Afficher des données dans le shell et parler à python
5 - Stocker des données dans des variables
6 - Calculer
7 - Les séries de données – une liste pour vos mesures
8 - Le test booléen – avec des si…
9 - Boucle bornée - les tâches répétitives mais ayant une fin
10 - Boucle non bornée – les tâches répétitives dont je ne connais pas le terme
11 - Les fonctions – pour faire comme en maths
12 - Présentation des bibliothèques – bienvenue dans l’Alexandrie du XXIème siècle
13 - Import de données d’un fichier csv
14 - Utilisation de fonctions en maths et calculs
15 - Visualisation des données avec matplotlib
16 - Faire de la physique avec scypi

Physique - Décroissance radioactive

Source

Extrait d'un manuel de physique. Le script du doc 2 ne fonctionne pas mais il donne des idées

"Comprendre" le script (qui ne fonctionne pas ;)

Les problèmes de ce script sont:

randint nécessite la bibliothèque random
plt.scatter et plt.show nécessite la bibliothèque matplotlib.pyplot

L'esprit du programme semble être:

J'ai N0 atomes radioactifs
Tant qu'il en reste :
- J'ajoute à ma liste L le nombre d'atome radioactif
- Boucle for
  - Je tire pour chaque atome la probabilité qu'il se désintègre (1/50) et je les compte avec s
  - A la fin de ce round de désintégration, donc en sortant de la boucle for, je dois faire mes comptes
- Je repars alors avec un nouveau nombre d'atomes radioactif et je recommence tant qu'il en reste
Pour le graphique je crée une liste t ayant le même nombre de valeurs que la liste L, t représente ici les n° des rounds

Des print() pour comprendre...

Soit 10 atomes radioactifs, pour faire simple et rapide.

import matplotlib.pyplot as plt
from random import randint
N=10
L=[]

while N>0:
    L.append(N)
    s=0
    print(N)# impression pour comprendre
    for i in range (N):
        print(i,s,N)# impression pour comprendre
        if randint(1,50)==1:
            s=s+1
    N=N-s
        
print("Evolution du nombre de noyaux restants: N = ",L)
t=[i for i in range (len(L))]

plt.plot(t,L,'.',color="blue")
plt.show()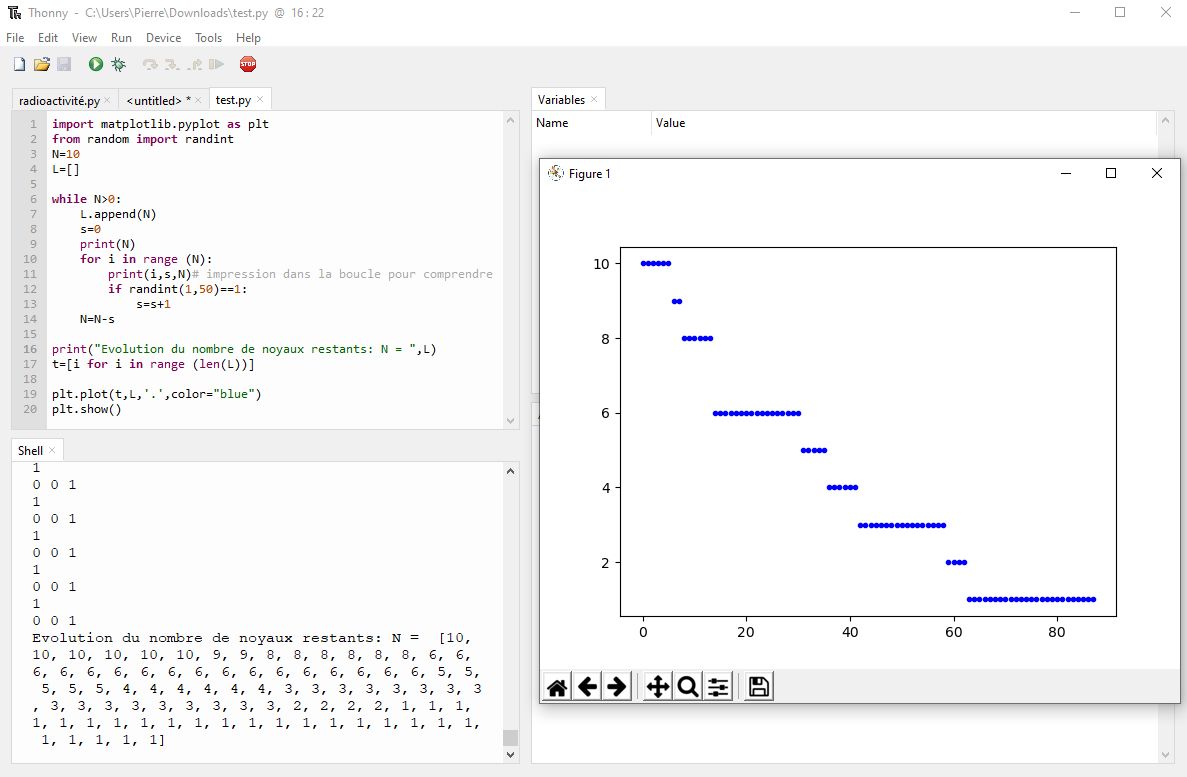

Je comprends :

Round 1 - 10 atomes rad / Aucune désintégration / Reste donc 10 atomes
Round 2 - idem
...
Round 6 - idem
Round 7 - 10 atomes rad / 1 désintégration / Reste donc 9 atomes
Round 8 - 9 atomes / Aucune désintégration / Reste donc 9 atomes
Round 9 - 9 atomes / 2 désintégrations / Reste donc 6 atomes
...

Script final

Vous pouvez le commenter maintenant ;)

import matplotlib.pyplot as plt
from random import randint
N=int(input("Saisir le nbre initial de noyaux en valeur entière (ex 10000): N0="))
L=[]

while N>0:
    L.append(N)
    s=0
    for i in range (N):
        if randint(1,50)==1:
            s=s+1
    N=N-s
        
print("Evolution du nombre de noyaux restants: N = ",L)
t=[i for i in range (len(L))]

plt.plot(t,L,'.',color="blue")
plt.show()

Physique - Mouvement sur un plan incliné

Source

Extrait d'un manuel de physique. Par respect pour le concepteur de ce script, je laisse les lignes ###TODO donc ce programme est à terminer! Il vous manque l'accélération ;)

Le fichier csv contenant les valeurs est en dessous, vous devez le télécharger et l'enregistrer dans le dossier qui contiendra votre programme python!
https://www.ipa-troulet.fr/cours/attachments/article/542/cylindre_plan_incline.csv

Le début du programme ne fonctionnant pas, j'ai utilisé pandas

import pandas as pd
mesures=pd.read_csv('cylindre_plan_incline.csv', sep=";",decimal=",",encoding="utf-8")
valeurs=mesures.values.tolist()

t=[];x=[];y=[];L=[t,x,y]

for i in range(len(valeurs)):
    t.append(valeurs[i][0]);x.append(valeurs[i][1]);y.append(valeurs[i][2])

Pour les curieux, j'ai trouvé ça aussi https://youtu.be/kvEtFBxDgqI

Un peu d'histoire pour comprendre

Si vous voulez vous amuser à reproduire cette expérience et à trouver la position des 4 clochettes, voici un lien vers un dossier zippé contenant :

un fichier wav qui fait "ding"
un début de script qui produit 4 "ding"

A vous de le modifier pour permettre par exemple à l'utilisateur de saisir 4 valeurs pour les x1... x4 afin d'entendre 4 ding à intervalles réguliers ;). Je précise que Galilée recherche une durée constante entre chaque clochette ;)))
Attention, ce script utilise la bibliothèque playsound, j'ai dû l'installer!

Dossier zippé: musique_galilee.zip

Script fonctionnel

import matplotlib.pyplot as plt
import pandas as pd
mesures=pd.read_csv('cylindre_plan_incline.csv', sep=";",decimal=",",encoding="utf-8")
valeurs=mesures.values.tolist()

t=[];x=[];y=[];L=[t,x,y]

for i in range(len(valeurs)):
    t.append(valeurs[i][0]);x.append(valeurs[i][1]);y.append(valeurs[i][2])

            
vx=[];vy=[];ax=[];ay=[]
for i in range (1,len(x)-1):
    vx.append((x[i+1]-x[i-1])/(t[i+1]-t[i-1]))
    vy.append((y[i+1]-y[i-1])/(t[i+1]-t[i-1]))
### TODO
#   A compléter
    
plt.subplot(2,1,1);plt.title("Vitesse")
plt.quiver(x[1:-1],y[1:-1],vx,vy,color="green")
plt.axis('equal');plt.plot(x,y,"ro")

plt.subplot(2,1,2);plt.title("Accélération")
### TODO
#   A compléter

plt.show()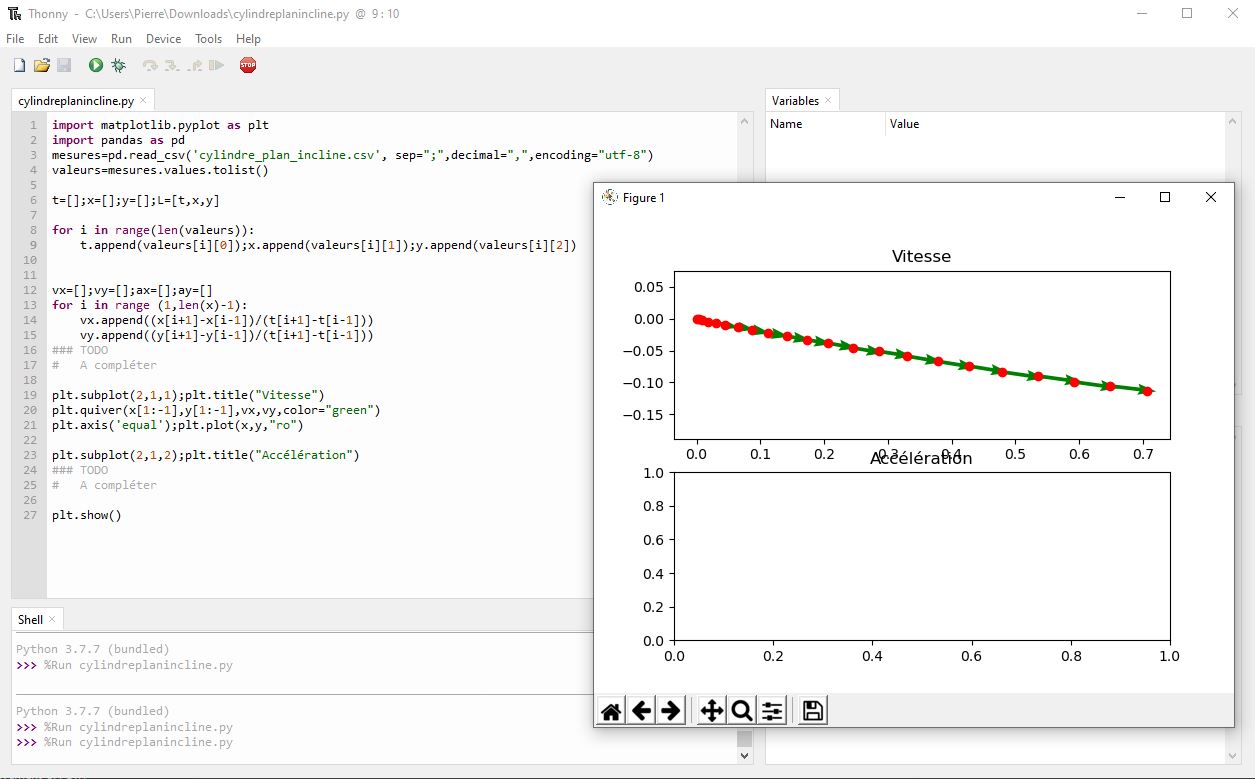

Comprendre le script

Lignes 1 et 2: import des bibliothèques
Lignes 3 et 4: récupération des données du fichier csv => j'obtiens une liste de nom "valeurs"
Ligne 6: déclaration de listes vides, une pour le temps, une pour les x et une pour les y. J'ai laissé la liste L qui est une liste contenant 3 sous-liste car elle était dans le script initiale, mais je ne m'en sers pas!
Lignes 8 et 9: découpe en tranche ;)
Ligne 12: déclaration de listes vides pour les composantes de la vitesse et de l'accélération
Boucle de la ligne 13:
- Calculs des vitesses et mise en boite
- TODO à faire pour les accélérations
Lignes de 19 à 21: représentation des vitesses. Vous chercherez le pourquoi du x[1:-1] car vous aurez besoin de ce concept pour l'accélération
Lignes de 23 à...: TODO à faire pour l'accélération en partant des vitesses. Vous ne m'expliquerez pas votre vx[truc:bidule] ;)
Ligne 27: affichage des graphiques (subplot c'est sous-graphique)

Chimie - Dosage d'une solution d'acide par la soude

Source

Extrait d'un manuel de chimie. Ce script n'a aucune erreur!

La théorie pour comprendre

Je retiens:

Une mole d'acide réagit avec une mole de base dans les proportions stœchiométriques
Je me méfie des unités - volume en mL!

Des print() pour comprendre...

import matplotlib.pyplot as plt
import numpy as np
C_B=0.2
V_A=5
V_E=15
C_A=C_B*V_E/V_A
n_A=C_B*V_E*1e-3

V_B1=np.linspace(0,V_E,V_E*1+1) # V_E*1+1 -valeur modifiée pour simplifier l'affichage!
n_a1=(C_A*V_A-C_B*V_B1)*1e-3
n_b1=C_B*V_B1*1e-3
n_B1=0*V_B1

V_B2=np.linspace(V_E,V_E*1.5,V_E*10+1)
n_a2=0*V_B2
n_b2=(0*V_B2+C_B*V_E)*1e-3
n_B2=C_B*(V_B2-V_E)*1e-3

print(V_E,V_E*10+1)
print("V_B1=",V_B1)
print("n_a1=",n_a1)
print("n_b1=",n_b1)
print("n_B1=",n_B1)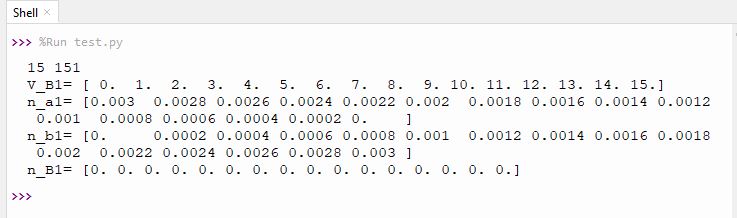

Je comprends:

V_E*10+1 me donnera 151 car je veux 151 valeurs dans le programme final
V_B1 est une liste (ici de 16 valeurs - V_E*1+1) de 0 à 15 tous les 1.0
n_a1, n_b1 et n_B1 sont aussi des listes puisque dans leurs relations se trouve V_B1!

Je dois comprendre aussi que mon dosage se découpe en 2 étapes:

Le versement progressif de la Base => neutralisation de l'acide => liste V_B1
Le versement progressif de la Base au delà de la neutralisation => ajout des HO- =>liste V_B2

J'anticipe le script final:

plt.plot pour les graphiques
Regroupement par couleur des éléments présents pour les 2 étapes donc pour les 2 listes V_B1 et V_B2

Script final

import matplotlib.pyplot as plt
import numpy as np
C_B=0.2
V_A=5
V_E=15
C_A=C_B*V_E/V_A
n_A=C_B*V_E*1e-3

V_B1=np.linspace(0,V_E,V_E*10+1)
n_a1=(C_A*V_A-C_B*V_B1)*1e-3
n_b1=C_B*V_B1*1e-3
n_B1=0*V_B1

V_B2=np.linspace(V_E,V_E*1.5,V_E*10+1)
n_a2=0*V_B2
n_b2=(0*V_B2+C_B*V_E)*1e-3
n_B2=C_B*(V_B2-V_E)*1e-3

plt.plot(V_B1,n_a1,color="blue",label="AH")
plt.plot(V_B1,n_b1,color="green",label="A-")
plt.plot(V_B1,n_B1,color="red",label="HO-")

plt.plot(V_B2,n_a2,color="blue")
plt.plot(V_B2,n_b2,color="green")
plt.plot(V_B2,n_B2,color="red")

plt.title("Evolution des quantités de matières des espèces \nen fonction du volume de solution titrante versée \nTitrage de l'acide lactique par la soude")
plt.legend(loc="upper right")
plt.xlabel("Volume de la solution titrante (en mL)")
plt.ylabel("Quantités de matières des espèces en solution (en mol)")
plt.grid()

plt.show()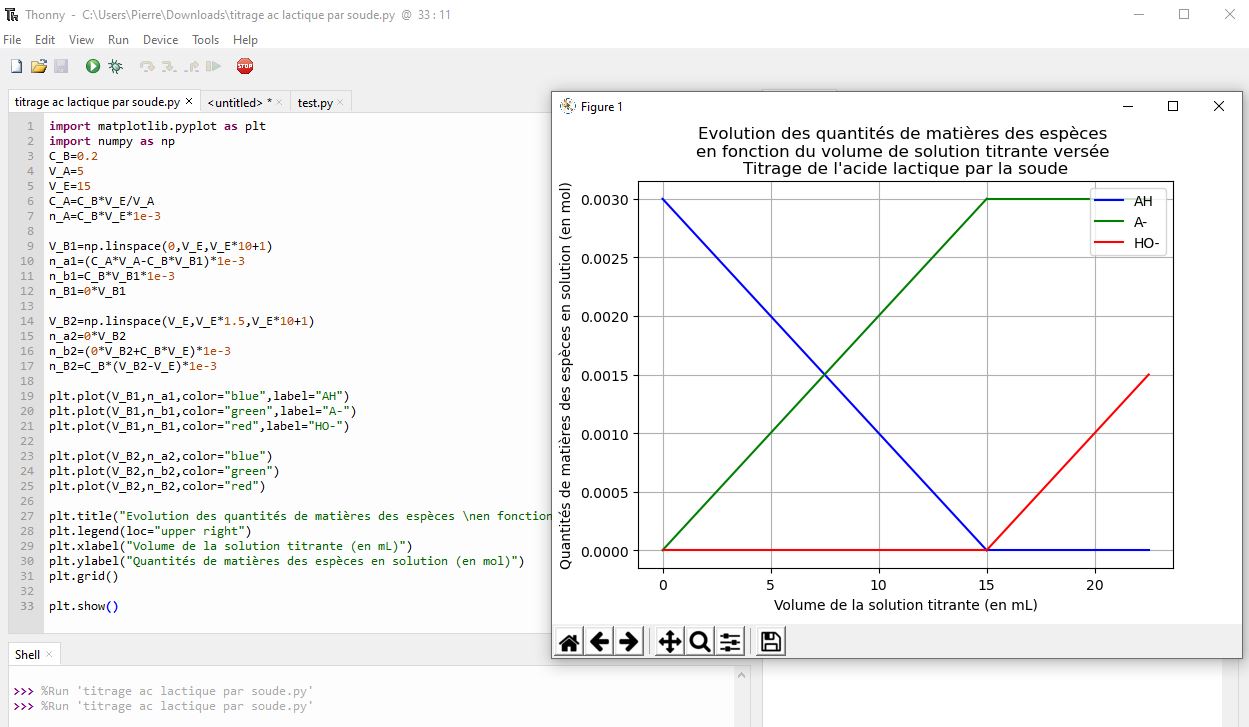

Maths - Evaluation d'une population à partir d'un échantillon

Source

https://github.com/exo7math/python2-exo7/blob/master/bigdata/bigdata-1.pdf

Voir l'activité 3 (La formule des tanks).
Plus d’info :
https://fr.wikipedia.org/wiki/Probl%C3%A8me_du_char_d%27assaut_allemand
Pour aller plus loin :
https://fr.wikipedia.org/wiki/Capture-marquage-recapture

Intérêt

L'exercice est impressionnant, avec 4 numéros de séries on peut estimer la taille d'un ensemble. C'est le problème des data d'ailleurs, car on ne peut s'avoir ce que les maths peuvent en extraire.

"En plein milieu de la seconde guerre mondiale les Allemands produisent un nouveau tank plus performant. Les Alliés s’inquiètent car ils ne savent pas combien de ces nouveaux tanks sont produits. Les services de renseignements estiment la production à 1500 tanks par mois.
Que disent les mathématiques ?
Les Alliés ont intercepté 4 tanks produits le même mois et qui portent les numéros :
143, 77, 198 et 32."

Sujet en pdf

L'image du dessous est cliquable et donne accès:

au support en pdf
à la correction des 3 premières parties (mais en cherchant un peu vous devez y arriver)
pour les questions 4 et 5, je vous laisse chercher mais que ne peut-on faire avec un for et un un peu de temps...
- solution du 4 - mais c'est triché

Aide

En plus de def pour la définition des fonctions demandées, j'ai utilisé :

max, len pour l'exo 1
la biblio numpy pour avoir la fonciton mean (calcul la moyenne) pour l'exo 2
et random, append, choice et remove pour l'exo 3, qui est le plus amusant ;)

Pièce(s) jointe(s)
COURS initiation python.odt	[ ]	3257 kB
COURS initiation python.pdf	[ ]	3120 kB
DOC_Manipulation_Matplotlib.pdf	[ ]	331 kB
DOC_Manipulation_Pandas.pdf	[ ]	1281 kB
DOC_numerique_python.pdf	[ ]	2225 kB
mesures.csv	[ ]	5 kB

Menu Principal

En ligne

Derniers articles

Term GEN - Remise à niveau python

Index de l'article

Objectif

Table des matières

Physique - Décroissance radioactive

Source

"Comprendre" le script (qui ne fonctionne pas ;)

Des print() pour comprendre...

Script final

Physique - Mouvement sur un plan incliné

Source

Un peu d'histoire pour comprendre

Script fonctionnel

Comprendre le script

Chimie - Dosage d'une solution d'acide par la soude

Source

La théorie pour comprendre

Des print() pour comprendre...

Script final

Maths - Evaluation d'une population à partir d'un échantillon

Source

Intérêt

Sujet en pdf

Aide

Derniers articles... de Bac Techno